資料的正規化(Normalization)及標準化(Standardization)
當我們在比較分析兩組數據資料時,可能會遭遇因單位的不同(例如:身高與體重),或數字大小的代表性不同(例如:粉專1萬人與滿足感0.8),造成各自變化的程度不一,進而影響統計分析的結果;為解決此類的問題,我們可利用資料的正規化(Normalization)與標準化(Standardization),藉由將原始資料轉換成無量綱(Dimensionless)的純量後,來進行數據的比較及分析。
資料的正規化(Normalization)是將原始資料的數據按比例縮放於 [0, 1] 區間中,且不改變其原本分佈。舉例來說,若我們現有兩組數據資料,分別表示 500 項商品的銷售量 Sample 1 及銷售額 Sample 2,如下圖所示,很明顯地,此兩組資料的單位不同,且數字上有著懸殊的差異,分別透過資料正規化後,兩組資料將同時轉換成純量縮放於 [0,1] 區間中,如下右圖所示;這樣的資料轉換,能排除資料單位的限制,提供我們一個相同的基準來進行後續比較分析。
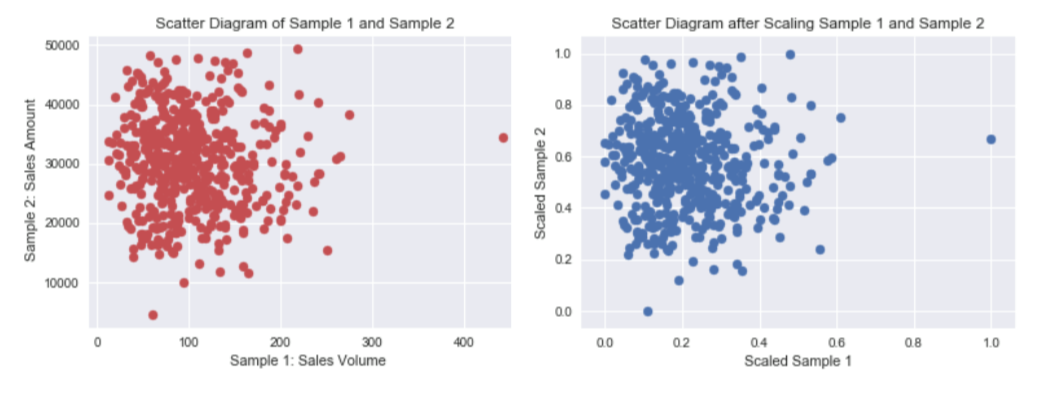
另一方面,資料的標準化(Standardization)可運用在機器學習演算法中,它能帶給模型下面兩個好處:
1. 提升模型的收斂速度
在建構機器學習模型時,我們會利用梯度下降法(Gradient Descent)來計算成本函數(Cost Function)的最佳解;假設我們現有兩個特徵值 x1 in [0,1] 與 x2 in [0,10000],則在 x1-x2 平面上成本函數的等高線會呈窄長型,導致需較多的迭代步驟,另外也可能導致無法收斂的情況發生。因此,若將資料標準化,則能減少梯度下降法的收斂時間。
2. 提高模型的精準度
將特徵值 x1 及 x2 餵入一些需計算樣本彼此的距離(例如:歐氏距離)分類器演算法中,則 x2 的影響很可能將遠大於 x1,若實際上 x1 的指標意義及重要性高於 x2,這將導致我們分析的結果失真。因此,資料的標準化是有必要的,可讓每個特徵值對結果做出相近程度的貢獻。
如何進行標準化及正規化?
下面我們介紹兩種常見的標準化及正規化方法:
(1) Z分數標準化(Z-Score Standardization)
假設資料的平均數與標準差分別為 μ 及 σ ,Z分數標準化可利用下列公式進行:
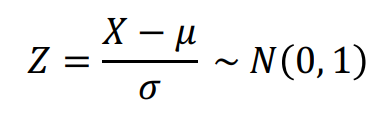
經 Z分數標準化後,資料將符合標準常態分佈(Standard Normal Distribution),轉換後的平均值=0、標準差=1,且用標準分數或稱 Z分數(Z-Score)來作為單位。Z分數標準化適用於分佈大致對稱的資料,因為在非常不對稱的分佈中,標準差的意義並不明確,此時若標準化資料,可能會對結果做出錯誤的解讀,另外,當我們未知資料的最大值與最小值,或存在超出觀察範圍的離群值時,可透過 Z分數標準化來降低離群值對整個模型的影響。
在實務操作時,我們可先分別計算資料的平均值及標準差,再代入上述公式完成標準化,另一種方法,我們可使用Scikit-learn 套件的preprocessing 模組來執行資料標準化,Python 程式語法為
preprocessing.scale(Data, axis=0, with_mean=True, with_std=True, copy=True) # Data 為原始資料
其中 with_mean及with_std 為布林值(Boolean)參數,若設定為False,則表示標準化後的平均值可不等於0與標準差可不等於1。這裡我們準備兩組資料 Sample 3 及 Sample 4,兩組資料的分佈情況及各別平均值、標準差,請詳下面圖表:
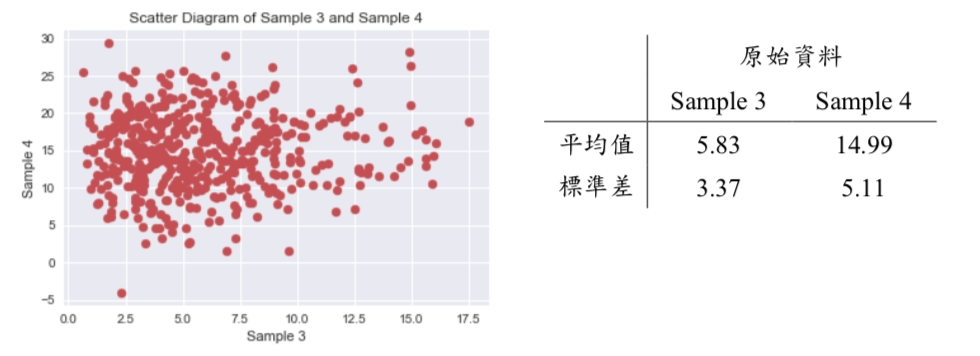
經觀察,Sample 3 及 Sample 4 的分佈範圍、平均值及標準差皆不盡相似,因此,我們可利用 Z分數標準化,將 Sample 3 及 Sample 4 皆轉換成平均值很近似 0及標準差很近似 1的資料;經 Z分數標準化後的分佈、平均值及標準差,請詳下面圖表:
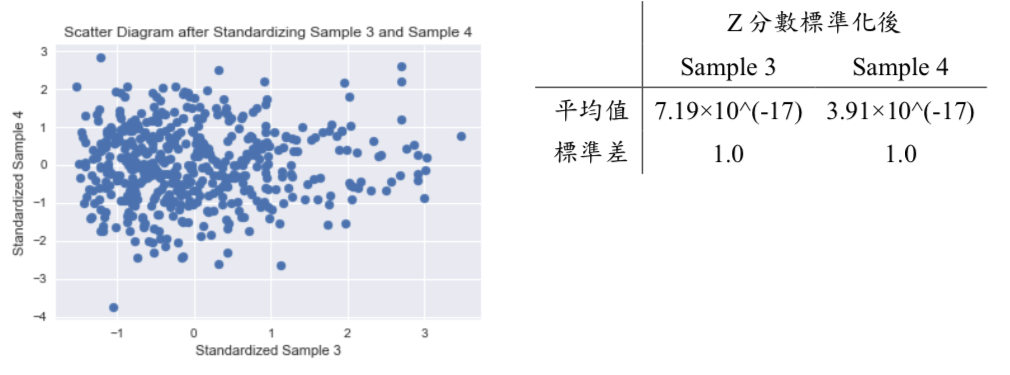
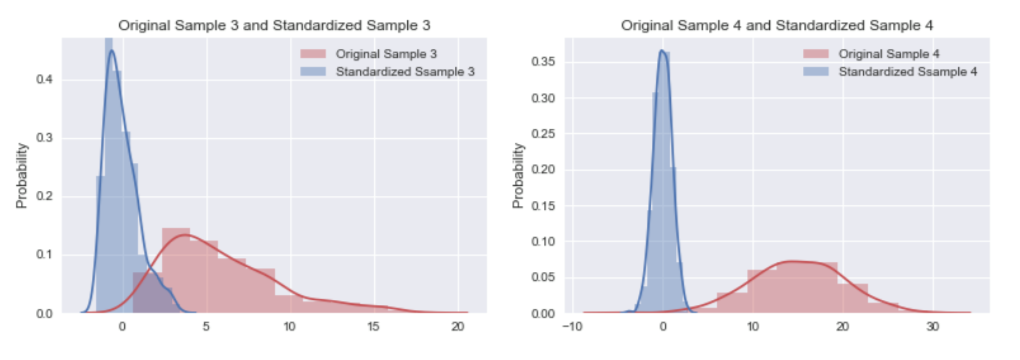
觀察轉換前後資料的分配情況,可發現資料皆轉換成符合標準常態分佈的態樣,Sample 3 及 Sample 4 轉換前後的分配情況,請詳下圖:
(2) 最小值最大值正規化(Min-Max Normalization)
最小值最大值正規化的用意,是將資料等比例縮放到 [0, 1] 區間中,可利用下列公式進行轉換:
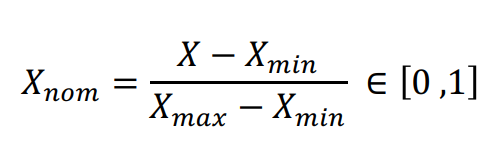
其中 Xmax 與 Xmin 分別為資料中的最小值與最大值。此種方法有一點需我們特別注意,即若原始資料有新的數據加入,有可能導致最小值 Xmin 及最大值 Xmax 的改變,則這時候我們需再重新定義公式中的 Xmin 及 Xmax。另外,若將轉換公式修改成下列:
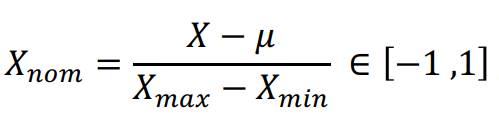
其中 μ 為資料的平均值,則資料將縮放到 [-1, 1] 區間中且平均值 = 0,我們稱這為平均值正規化(Mean Normalization)。
在實務操作最小值最大值正規化時,我們可使用 Scikit-learn 套件的MinMaxScaler 物件執行;首先,設定我們要縮放到的區間上下界,之後再呼叫 fit_transform( ) 函數來執行,Python 語法為
Min_Max_Scaler = preprocessing.MinMaxScaler( feature_range=(0,1) ) # 設定縮放的區間上下限 MinMax_Data = Min_Max_Scaler.fit_transform( Data ) # Data 為原始資料
這裡我們另準備兩組資料 Sample 5 及 Sample 6,這兩組資料的分佈情況及各別平均值、標準差,請詳下面圖表:
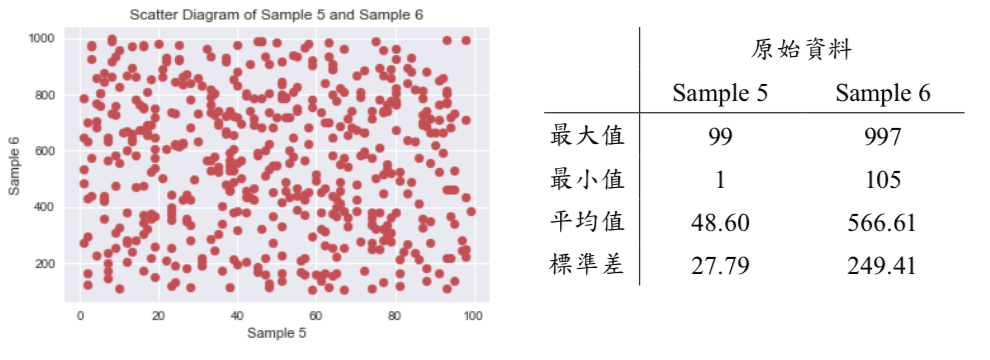
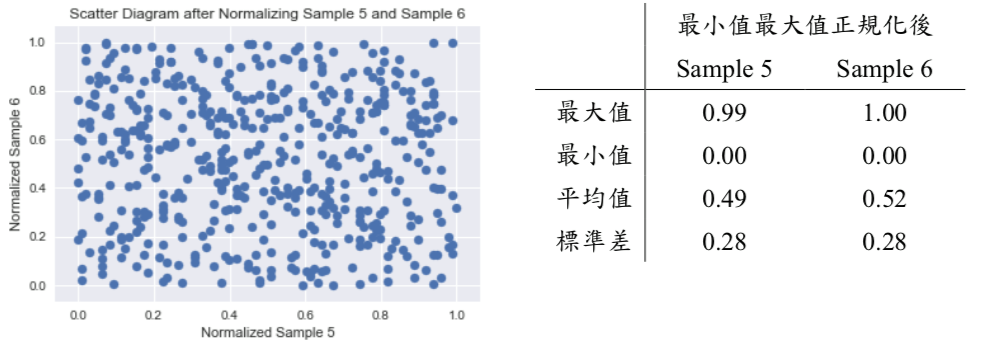
經觀察,Sample 5 及 Sample 6 的最小值、最大值、平均值及標準差皆有著明顯的差異,透過最小值最大值正規化,將兩組資料皆縮放於 [0, 1] 區間中,正規化後的分佈情況、最小值及最大值,請詳下面圖表:
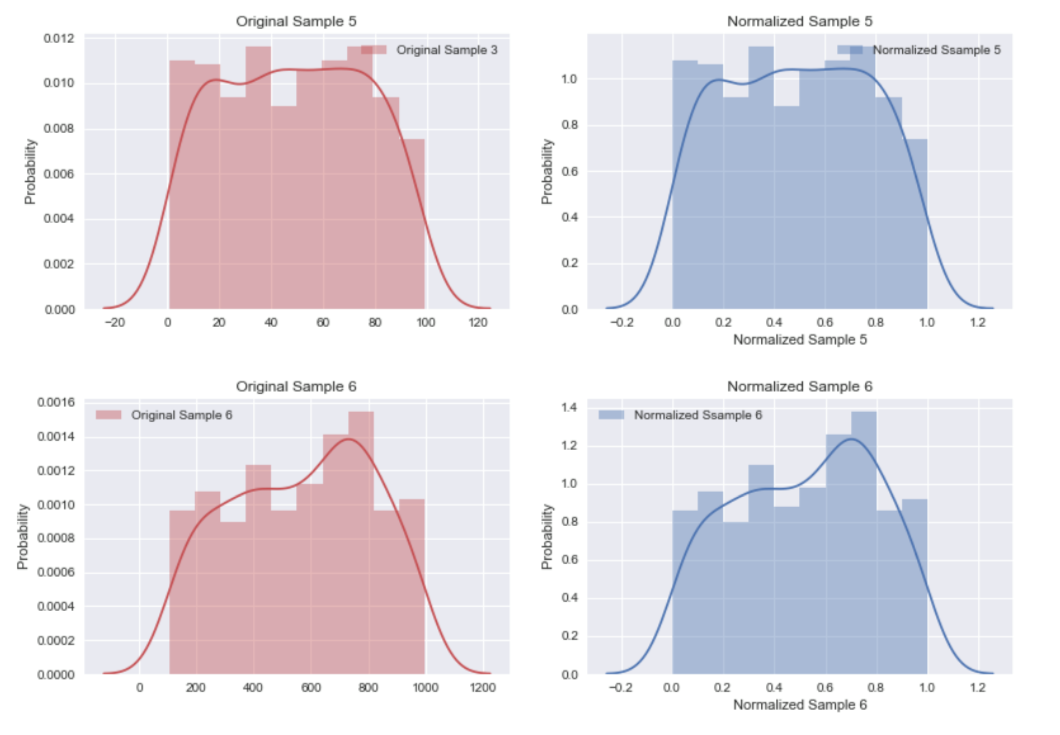
藉由觀察 Sample 5 及 Sample 6 各自正規化前後的分佈,請詳下圖(紅色為正規化前,藍色為正規化後),我們將瞭解到最小值最大值正規化僅將資料等比例縮放進 [0, 1] 區間中,但並不會改變原本的分佈情況。
總結:
在分析不同的資料時,為了排除彼此間單位的不同或數據的極大落差,我們可利用資料的標準化(Standardization)或正規化(Normalization),以便後續的分析及比較;資料的標準化,能將原始資料轉換成符合標準常態分佈的樣態( 平均值=0、標準差=1 ),而正規化則能將資料在保持原始的樣態下縮放入 [0,1] 區間中。
針對本文的內容,若讀者們有發現任何的錯誤或疑問,非常歡迎您來信給予建議及討論,讓我們一同來學習成長!
團隊信箱:AI.Free.Team@gmail.com
作者信箱:yenlinwu1112@gmail.com