深度學習 - 學習筆記(三)
本學習筆記課程為 Coursera DeepLearning.ai 推出之深度學習專項課程,學習筆記摘要自 AI . FREE Team 讀書會,透過學習筆記讓讀者認識深度學習。(進度:Course 1/Week 3)

一、線上課程資訊
課程名稱:深度學習專項課程 (Deep Learning Specialization)
課程教授:吳恩達 教授 (Andrew Ng)
課程主題:類神經網絡與深度學習 (Neural Network and Deep Learning)
二、課程內容
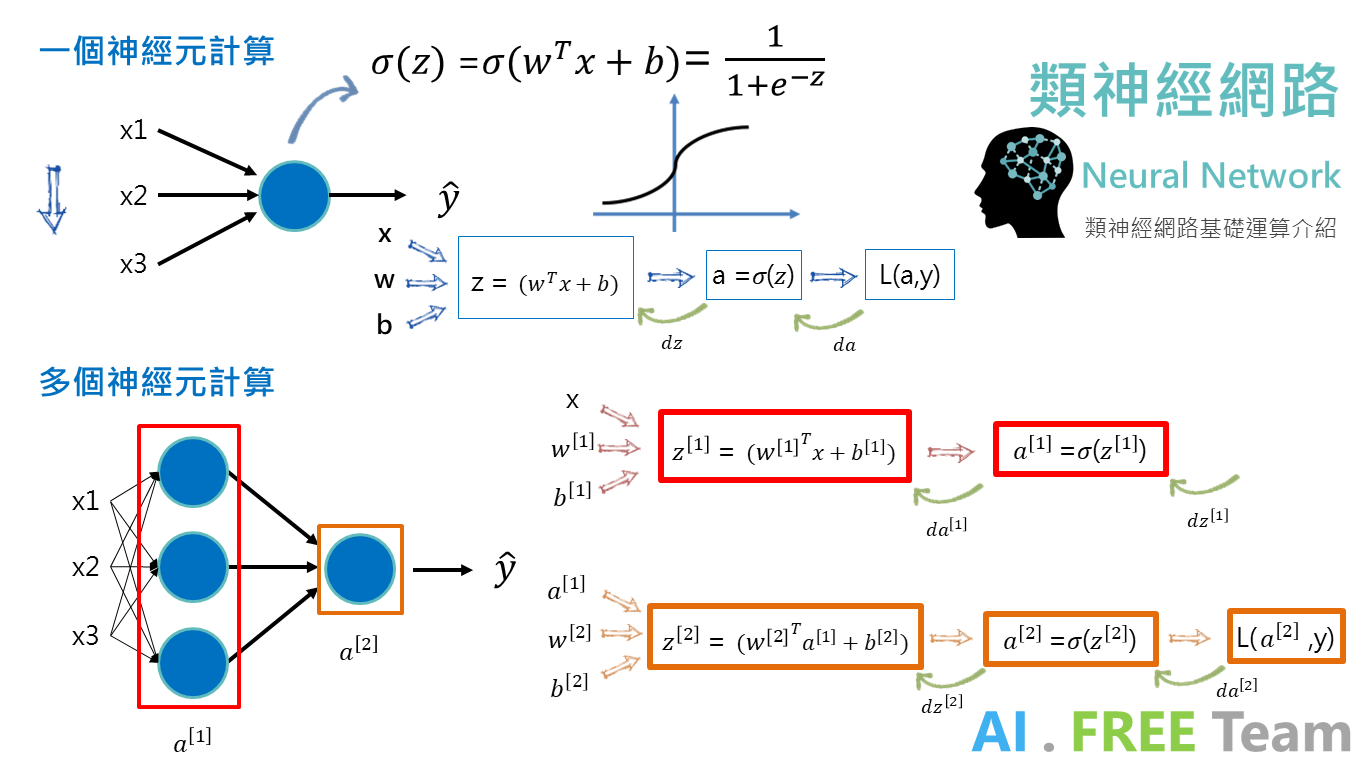
類神經網絡(Neural Network) 是由多個神經元 (Neurons) 所組成,從上方示意圖及計算公式可以發現:每個神經元就好像是一個 Logistic Regression,先進行向前傳播(Forward Propagation)→啟動函數(Activation Function)→向後傳播(Backward Propagation)。
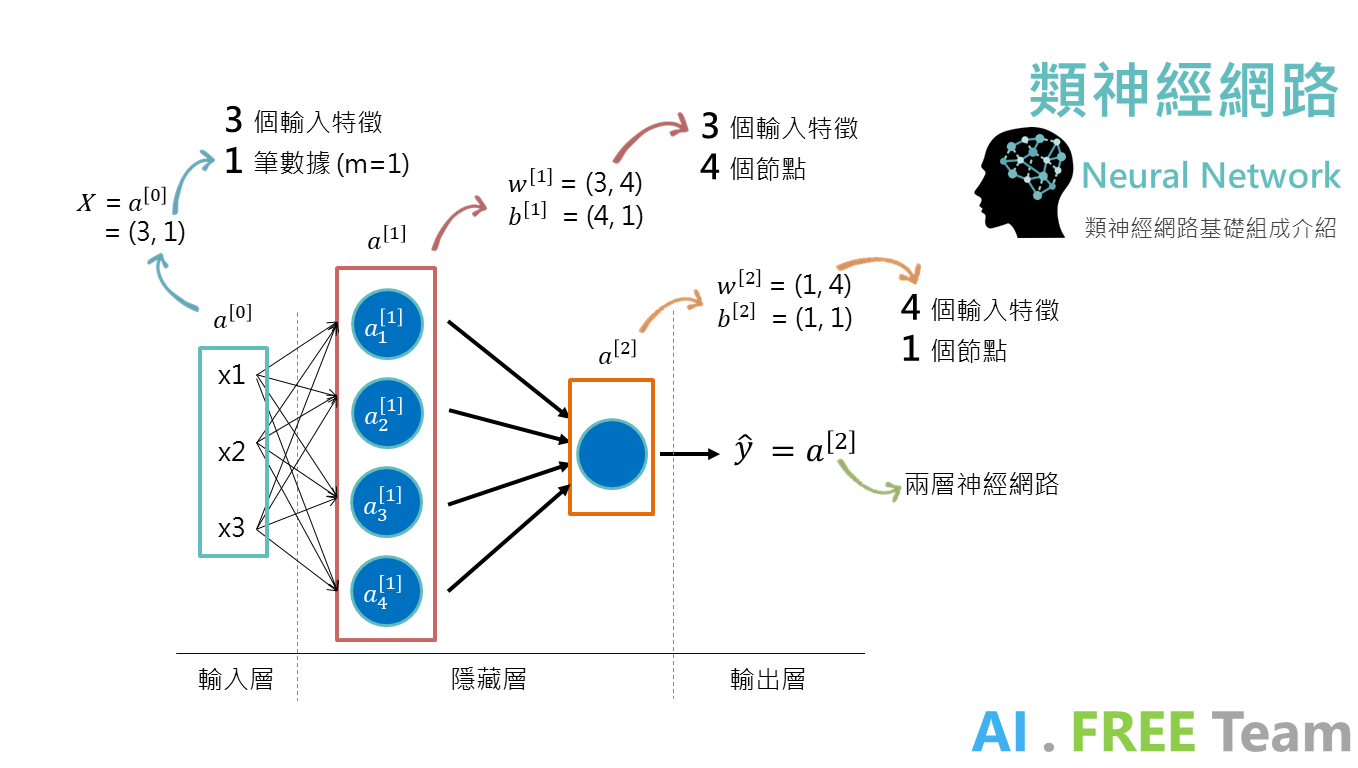
以上圖為例,Input Data 也就是 X ,我們稱作「輸入層 - a[0]」;Output Data 即 Y,稱作「輸出層」,而中間運算的神經元,我們稱作「隱藏層」。
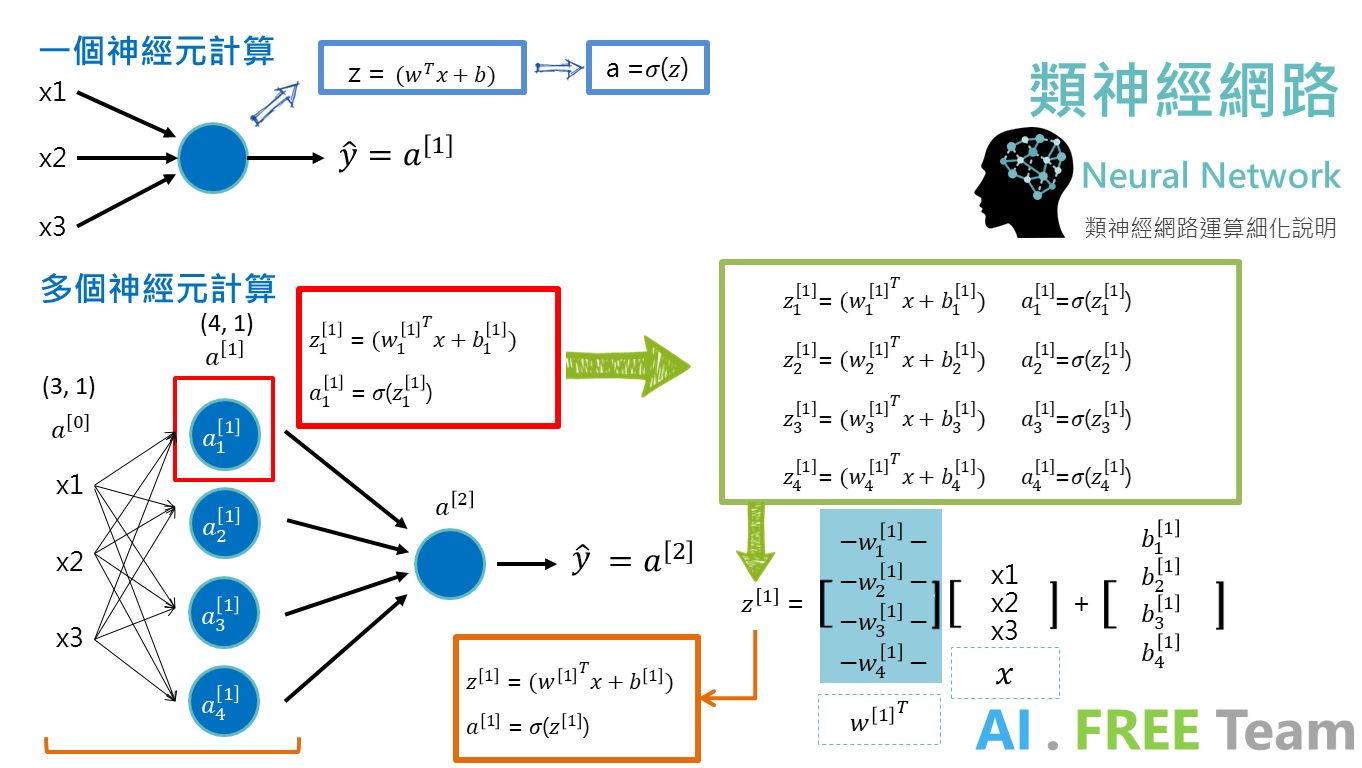
類神經網絡運算
在進行類神經網絡運算時,每個神經元都會進行其運算(向前傳播 + 啟動函數),而當我們在開發類神經網絡的過程,為了優化運算效率,我們會將每個神經元的權重進行堆疊(如右下角 w[1].T),而每個神經元的偏差也會進行堆疊以矩陣的方式呈現,因此進行類神經網絡運算時,會大量運用繁複的矩陣運算,而上圖橘框則為矩陣運算的簡易呈現。(w[1] : 第一層權重、b[1]:第一層偏誤)
在進行神經網絡運算時,矩陣的大小 (shape) 常常使開發者混淆;以上圖為例:
輸入層 3 個特徵值(x1, x2, x3)、僅一筆資料(m=1),因此 shape = (3, 1)
第一層隱藏層,輸入 3 個特徵值、有 4 個神經元,故權重( w[1] ) 的shape = (3, 4)
第二層隱藏層,輸入 4 個特徵值、有 1 個神經元,故權重( w[2] ) 的shape = (4, 1)
每個神經元都各自有偏差(bias),因此 b[1] shape = (4, 1)、b[2] shape = (1, 1)
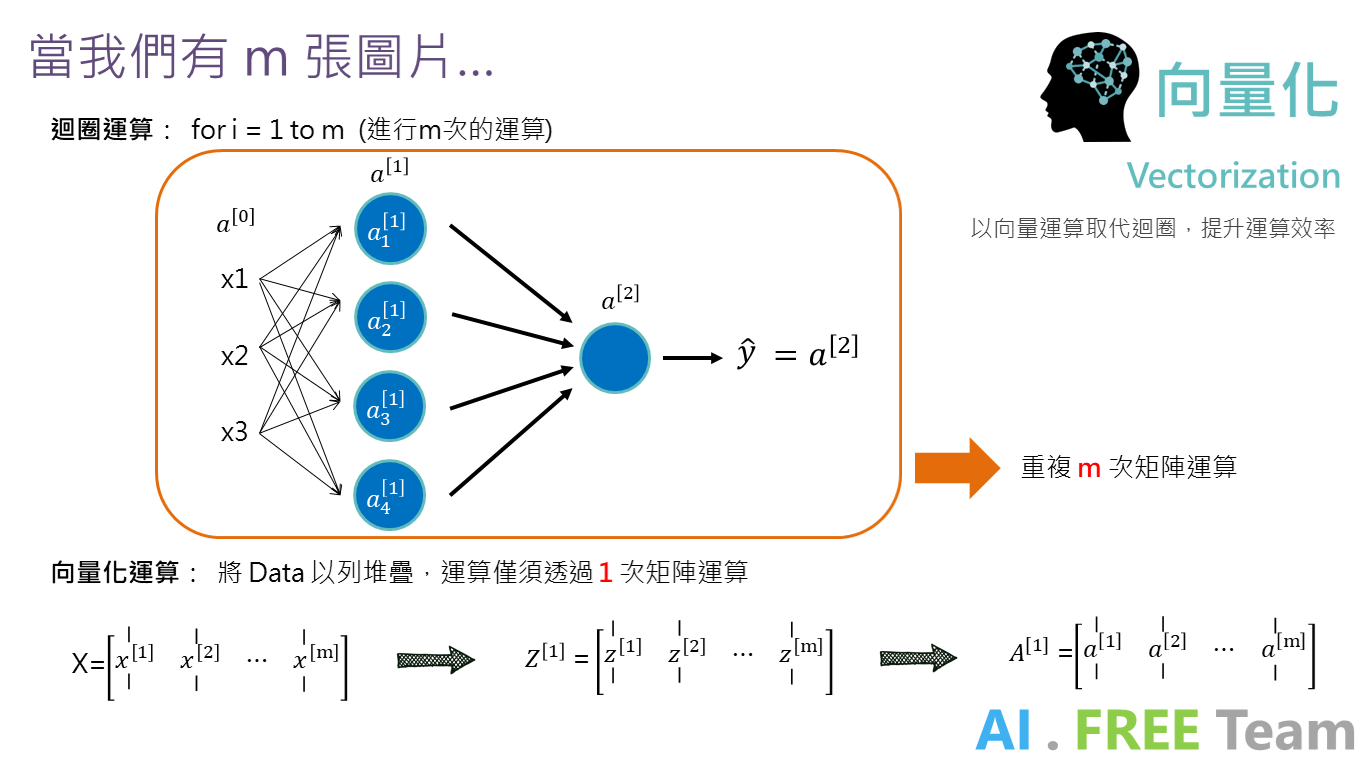
可以用迴圈進行計算,為何需要矩陣運算?
在程式開發過程中,進行矩陣運算相較利用迴圈進行運算來的快速,因此在進行開發「深度學習」時,矩陣運算能夠大幅提升運算效率。
因此,呈上圖,我們透過將每個神經元權重、偏誤的堆疊形成矩陣,並透過「向量化」將大量的訓練範例 (m) 轉換成一個大矩陣,再行矩陣運算,便能優化電腦運算的效率。
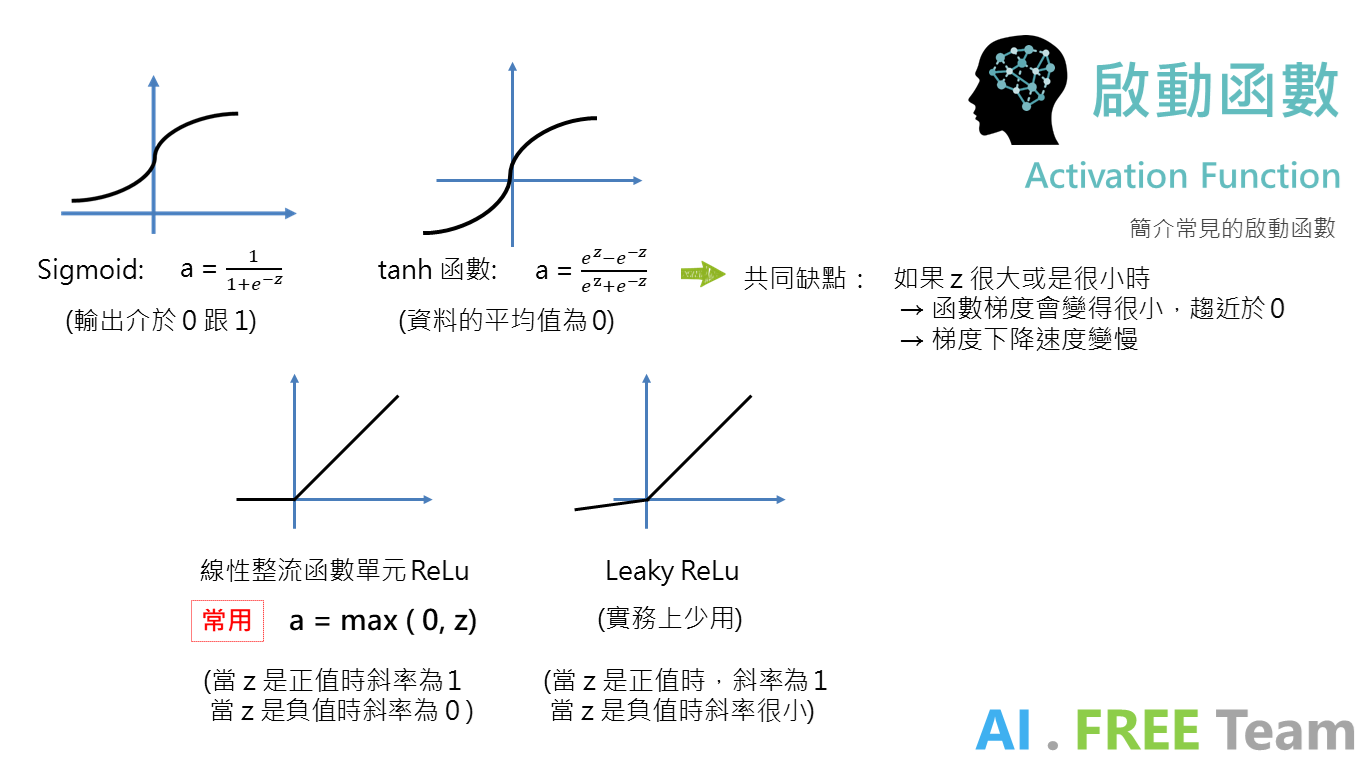
以上四個常見的啟動函數,其中 ReLu 較常使用在神經元間數據的運算,sigmoid 函數則較常出現在輸出前一層的啟動函數。
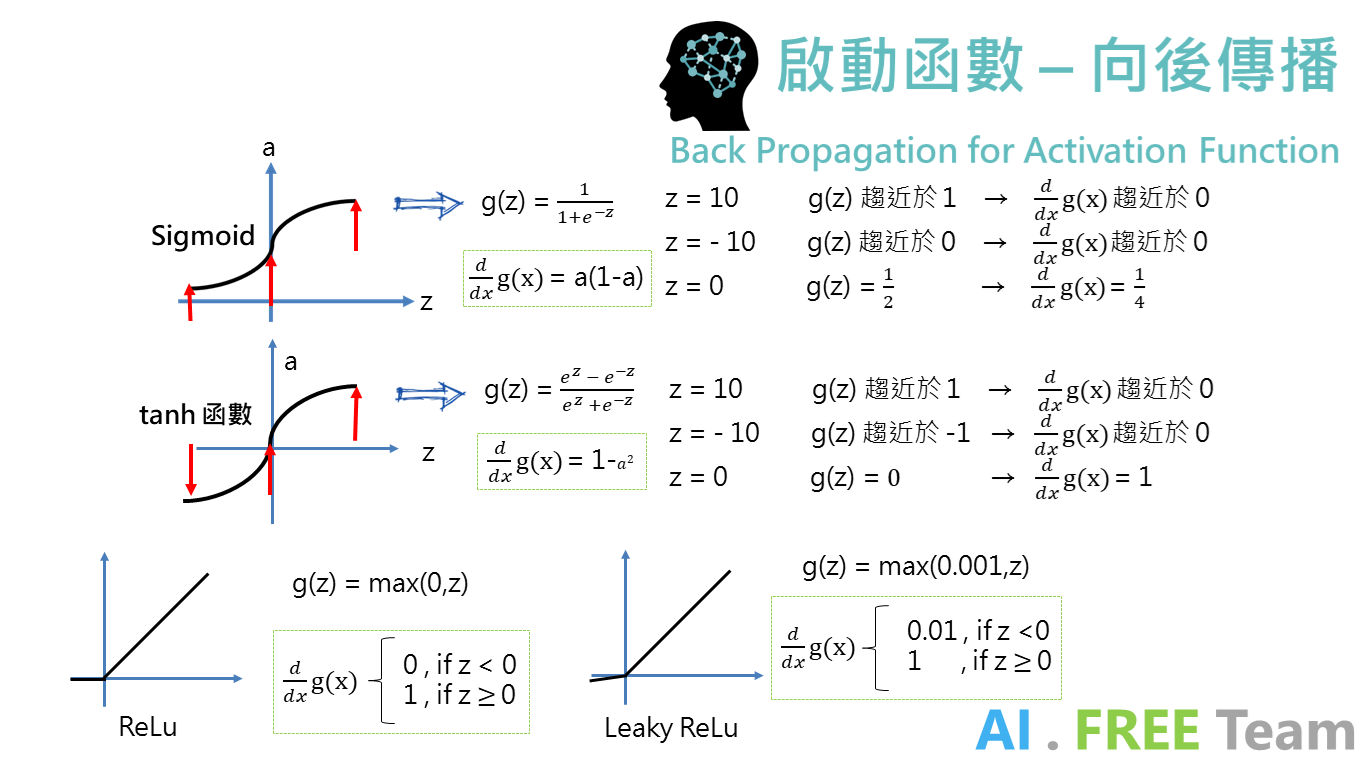
(本文不進行推導啟動函數的向後傳播運算,淺綠色框即為各函數微分後的公式)
若對於數學推導有興趣的讀者,歡迎參考下列影片:

為什麼需要非線性啟動函數?
因為線性函數之間的組合(乘積),仍為線性函數(簡易推導如上),會造成:
隱藏層失去意義 (即使疊了100層,效果如同1層)
以上統整自人工智慧自由團隊 - 深度學習專項課程讀書會,歡迎未來有興趣一起參與學習的朋友們,一起追蹤我們粉絲專頁、加入學習社團,並持續關注 AI . FREE Team 部落格,如有進一步問題或是交流需求,歡迎透過粉專 or email 聯絡我們喔!(AI.Free.Team@gmail.com)
相關資訊:
認識自由團隊:https://goo.gl/D2in5A
加入學習社群:https://goo.gl/k98CBy
企業合作專區:https://goo.gl/osGHhK
自由學習平台:https://goo.gl/ALVKKF
【AI.Free Team 介紹影片】
https://www.youtube.com/watch?v=nEOi9qk35KA