深度學習 - 學習筆記(二)
本學習筆記課程為 Coursera DeepLearning.ai 推出之深度學習專項課程,學習筆記摘要自 AI . FREE Team 讀書會,透過學習筆記讓讀者認識深度學習。(進度:Course 1/Week 2)

一、線上課程資訊
課程名稱:深度學習專項課程 (Deep Learning Specialization)
課程教授:吳恩達 教授 (Andrew Ng)
課程主題:類神經網絡與深度學習 (Neural Network and Deep Learning)
二、課程內容
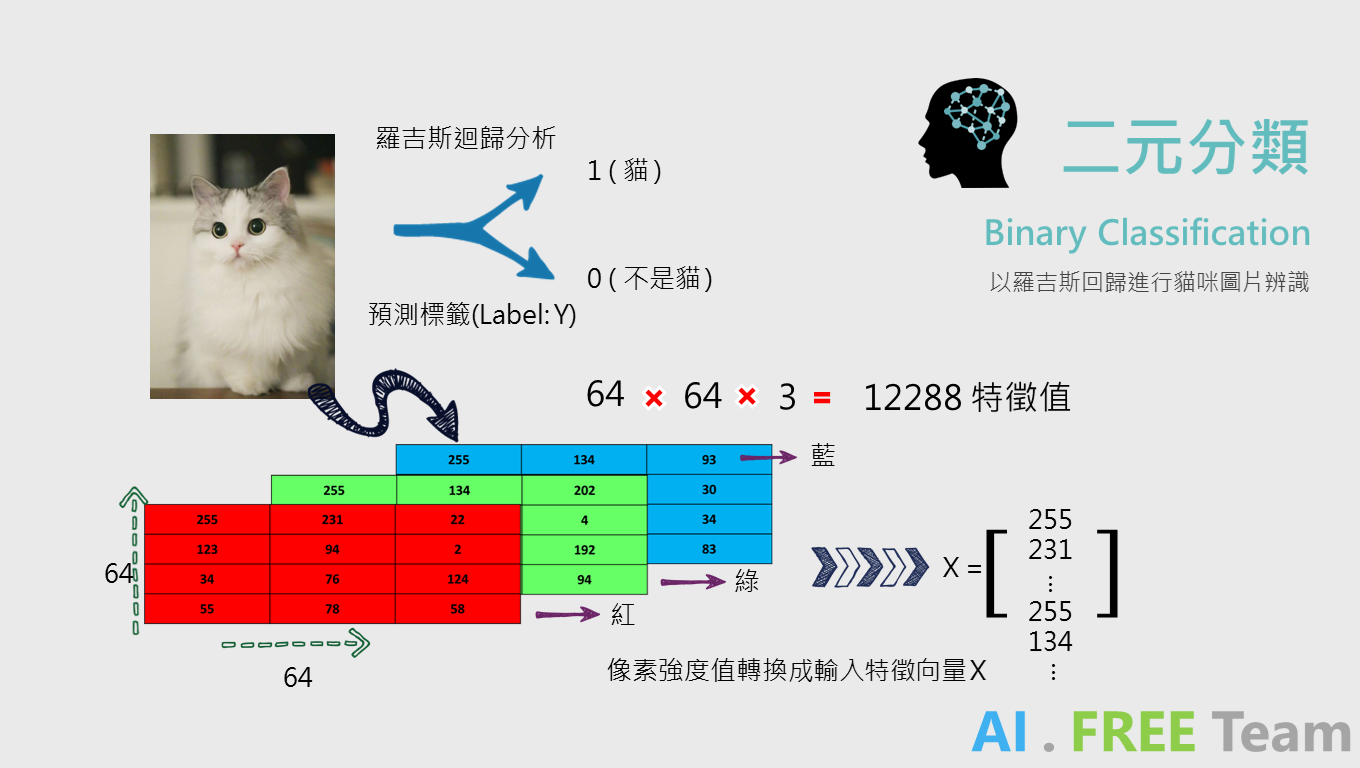
二元分類 (Binary Classification) 顧名思義即為將數據分成兩類的演算法,例:
以羅吉斯回歸進行喵咪圖片辨識,透過標籤數據 (Label) 來進行判別是否為貓咪 ( 1:(貓) ; 0:(不是貓) ),為了使電腦能夠判讀圖片,我們必須先將一張 64 * 64 pixels 的圖片轉換成 RGB 數值矩陣,再轉換成一 (12288 * 1) 的矩陣,以利後續數據丟入模型訓練。
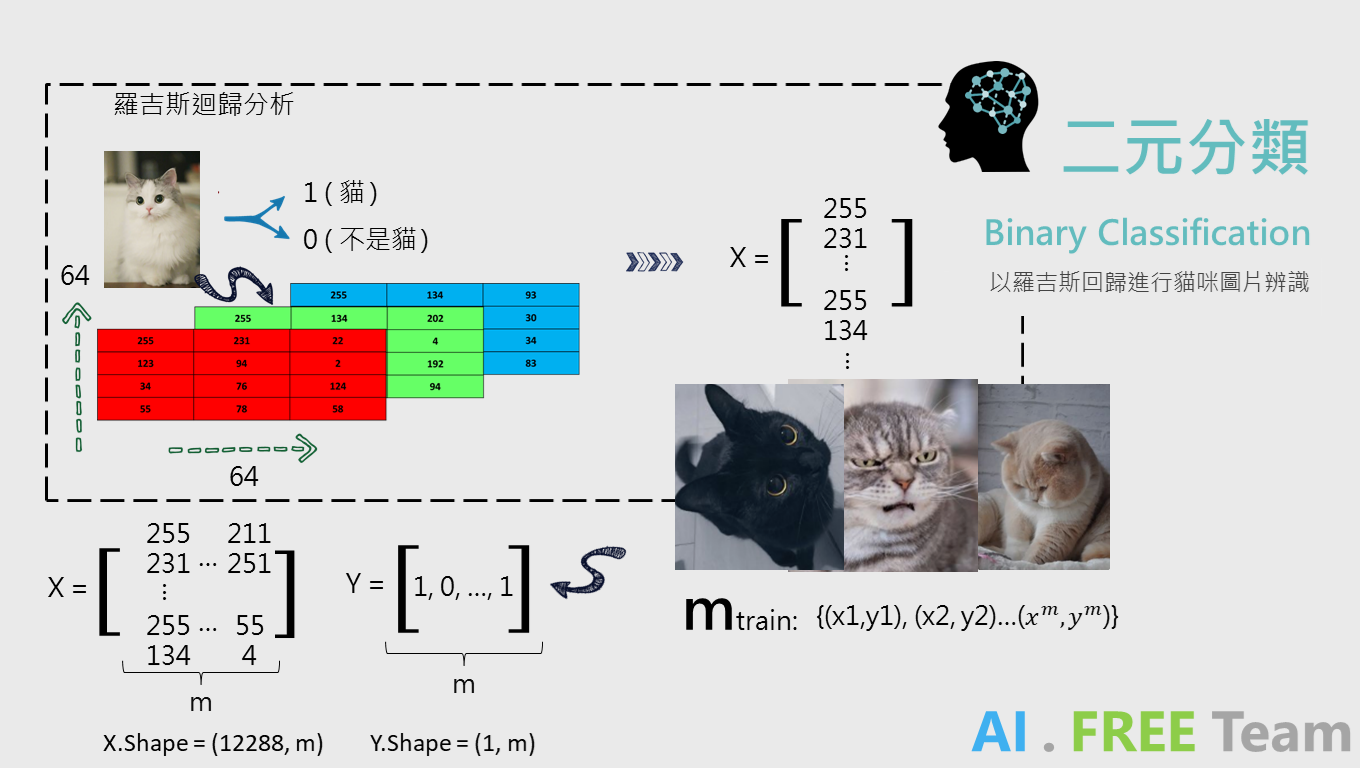
在進行機器學習時,資料科學家會蒐集大量的數據,承上例,假使我們有 m 張訓練集的圖片,數據將會有 m 個 12288 * 1 的矩陣及 m 個標籤(即 Y ,是否為貓咪),而為了機器學習運算上的效率,我們會將 m 筆數據進行合併 ( X 矩陣將由 12288 * 1 改變成 12288 * m;而標籤 Y 則會由單一數值變成 1 * m 的矩陣),再透過矩陣運算進行機器學習。

羅吉斯回歸如何運作?
以數學模型方式做解釋:在輸入 X 的情況下,輸出 Y=1 的機率為何?
若以辨識貓咪的圖片解釋:在輸入一張圖片的情況下,判別是貓的機率為何?
而我們的計算公式為 Y =σ( WT * X + b) (承上述,X 即為 12288 * m的矩陣、Y 為 1 * m的矩陣),而 W 則稱作權重(weights)、b 為偏誤(bias),σ 符號則稱作 sigmoid 函數。
用簡單的描述,讀者們可以先將「Z = WT * X + b」拆解出,並想像為 y = ax + b (傳統線性回歸)的公式,a 和 WT 便是係數(斜率),而 b 則為截距;透過此線性方程式計算後,我們可以得到 Z 值。 ( WT 上的 T 代表矩陣轉置,轉置的原因為:原始權重(W)的矩陣為 (12288 * 1),故轉置後 WT (1*12288) 便能與 X進行運算 )
得到 Z 值後,我們再將 Z 丟入 Sigmoid 函數,便能得到判別是否為貓的機率 (Y)。(為何使用 Sigmoid 函數?透過 Sigmoid 函數計算能將輸出數值投射在 0 到 1 之間,恰好等於「機率」的分佈。)

初步的計算出預測值後,透過「損失函數」計算標籤 Y (Label) 與 預測值(Y-hat)的差異,進而去計算「成本函數」衡量目前模型的表現(數值越大,表示模型預測出來的結果與實際狀況差異越大),我們目標即是最小化「成本」。(如上圖所示,成本函數最低點)
(註:此部分不細述損失函數公式推導,請參考下列影片 or 其他文章說明)
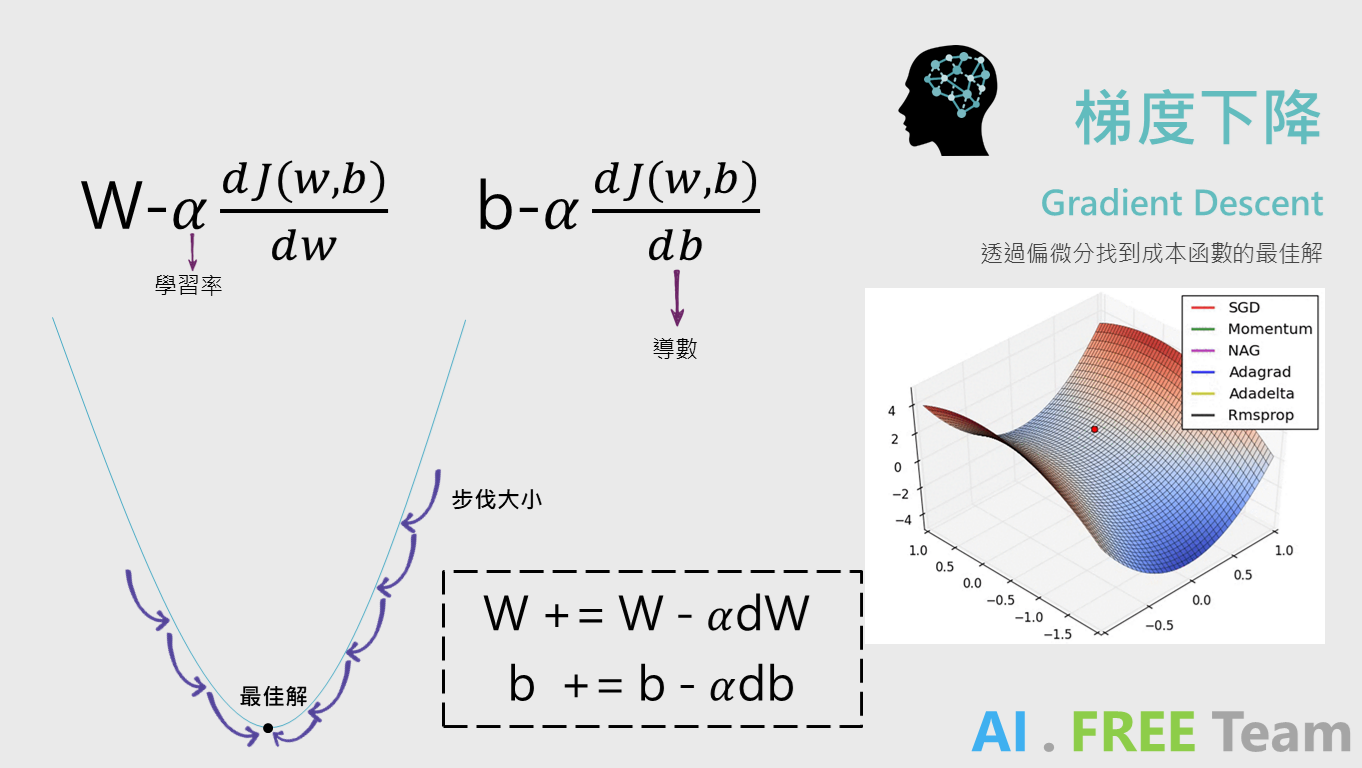
計算出成本函數後,我們需要透過梯度下降(偏微分)來找到「最佳解」。
簡易說明:偏微分能找出「參數」變化量對成本函數的影響大小。(參數:W, b)
如同對位移的公式微分可以得到速度、對速度的公式微分可以得到加速度...等概念。
因此透過偏微分,找到參數對於成本函數的影響大小後,乘上α (學習率)來進行調整參數。
(本文不細述公式推導,若針對偏微分有不理解的同學,歡迎參考 Andrew 教授的影片)
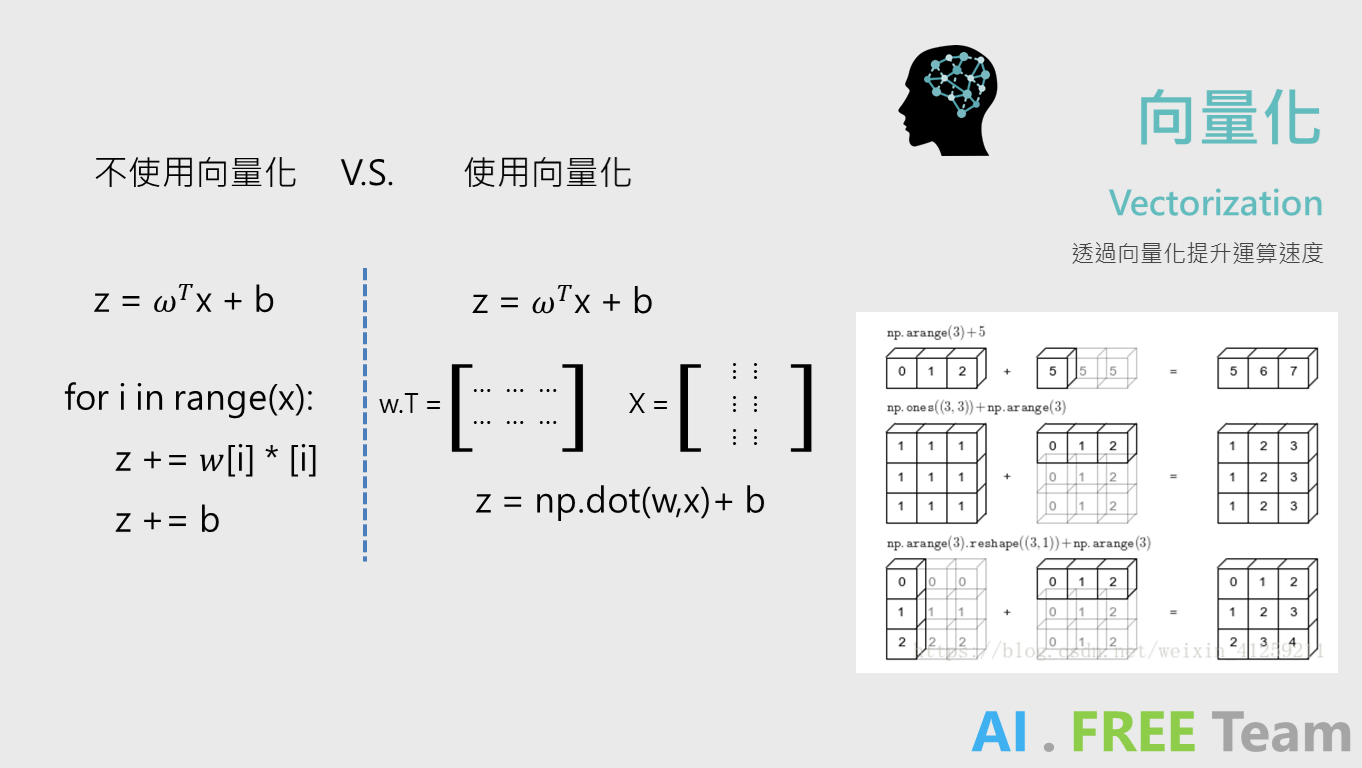
為什麼需要向量化?
相較使用 for-loop 進行線性方程式的運算,透過向量化進行矩陣運算能夠大幅節省運算時間。
Python 相關的開發套件(numpy) 便是針對矩陣運算所開發出來的套件,不僅能大幅減少進行開發演算法的時間,也有許多不錯的功能。( 例:Broadcasting ,請參考以下影片)
以上統整自人工智慧自由團隊 - 深度學習專項課程讀書會,歡迎未來有興趣一起參與學習的朋友們,一起追蹤我們粉絲專頁、加入學習社團,並持續關注 AI . FREE Team 部落格,如有進一步問題或是交流需求,歡迎透過粉專 or email 聯絡我們喔!(AI.Free.Team@gmail.com)
相關資訊:
認識自由團隊:https://goo.gl/D2in5A
加入學習社群:https://goo.gl/k98CBy
企業合作專區:https://goo.gl/osGHhK
自由學習平台:https://goo.gl/ALVKKF
【AI.Free Team 介紹影片】
https://www.youtube.com/watch?v=nEOi9qk35KA