
(圖片來源)

(Author: Dr. Wu - 彥霖 博士;Editor: Ken;Date of published: 2019/12/3)
這篇文章主要是與資料科學初心者們,分享機器學習的基本分析流程,透過 Kaggle 上鐵達尼號生存預測比賽,手把手從探索性數據分析(Exploratory Data Analysis)認識資料,到特徵工程(Feature Engineering)處理欄位的缺漏值、離群值等,最後,我們建立一個隨機森林(Random Forest)模型來預測資料。
本文章的用意,除期許能讓機器學習的初心者們有基礎概念外,同時提供幾個分析時常使用的 Python 程式碼,讓初心者們能夠更快速上手實作,若已有一定基礎的讀者們,則可再結合 Kaggle 討論區中的文章,更深入來優化整個分析過程。
分析主題: Titanic: Machine Learning from Disaster (第一次使用需註冊帳號、下載 Data)
(實作教學 Github;文末附上貼心 Colab 實作教學)
起手式,我們先載入分析過程中所需要用到的套件:
#pip install sklearn import pandas as pd import numpy as np # 繪圖相關套件 import matplotlib.pyplot as plt %matplotlib inline import matplotlib.gridspec as gridspec import seaborn as sns plt.style.use( 'ggplot' ) # 標籤編碼(Label)、獨熱編碼(OneHot) from sklearn.preprocessing import LabelEncoder, OneHotEncoder # 決策樹(Decision Tree) from sklearn.tree import DecisionTreeClassifier # 隨機森林(Random Forest) from sklearn.ensemble import RandomForestClassifier from IPython.display import display import warnings warnings.filterwarnings( 'ignore' )
上傳資料 (Optional - Colab 使用者)
透過 Kaggle 資料競賽網站,下載鐵達尼號資料集。(Kaggle)
(點擊 "Download All" 後解壓縮,上傳 gender_submission.csv, test.csv , train.csv)
※ 可一次上傳或分批上傳,上傳成功後,點擊左方 "Files" 欄位,即可看到上傳的檔案。 ※
from google.colab import files uploaded = files.upload()
匯入資料
透過 pandas 匯入訓練集與測試集資料,並利用 shape 得知資料的維度:
訓練集有 891 筆資料、12 個特徵欄位;
測試集有 418 筆資料、11 個特徵欄位;其中,訓練集較測試集多了判別乘客罹難或生還的特徵欄位 Survived,0 表示罹難者,1 表示生還者。
df_train = pd.read_csv('train.csv')
df_test = pd.read_csv('test.csv')
submit = pd.read_csv('gender_submission.csv')
print( f'train {df_train.shape}' )
display( df_train.head() )
print( f'\ntest {df_test.shape}' )
display( df_test.head() )欄位型態(Column Types)
我們透過自定義的函數 Col_Types,觀察訓練集與測試集共同的特徵欄位型態,數值型態的特徵欄位有 6 欄,非數值型態的特徵欄位有 5 欄,另外,Survived 欄位為數值型態。
# 定義判別欄位型態的函數 def Col_Types( Data ): Column_Types = Data.dtypes.to_frame().reset_index() # 判別每個欄位的型態 Column_Types.columns = ['ColumnName','Type'] Column_Types.sort_values( by='Type', inplace=True ) return Column_Types
display( Col_Types(df_train) )
缺漏值(Missing Values)
在分析資料之前,我們還需先檢視資料是否存有缺漏值(Missing Values),如果欄位存有缺漏值,之後在特徵工程(Feature Engineering)的過程中,我們可視欄位中缺漏值的比例或對預測值的相關性,決定填補或排除此欄位的處理方法。
透過我們自定義的函數 Missing_Counts ,發現 Embarked、Fare、Cabin、Age 欄位有缺漏值,當中, Cabin 欄位的缺漏情況最為嚴重,訓練集中約有 77%、測試集中約有 78% 的缺漏值,其次為 Age 欄位,訓練集中約有 20%、測試集中約有 21% 的缺漏值。
# 定義用來統計欄位缺漏值總數的函數
def Missing_Counts( Data ) :
missing = Data.isnull().sum() # 計算欄位中缺漏值的數量
missing = missing[ missing>0 ]
missing.sort_values( inplace=True )
Missing_Count = pd.DataFrame( { 'ColumnName':missing.index, 'MissingCount':missing.values } ) # Convert Series to DataFrame
Missing_Count[ 'Percentage(%)' ] = Missing_Count['MissingCount'].apply( lambda x:round(x/Data.shape[0]*100,2) )
return Missing_Countprint( 'train :' ) display( Missing_Counts(df_train) ) print( 'test :' ) display( Missing_Counts(df_test) )
統計量(Statistic)
利用 describe( ) 函數,我們可得到每個數值型態欄位的統計量,其用意是為往後我們在觀察欄位是否存有離群值(Outlier)時,作為一個判斷的參考依據,另外,也可用來觀察每個欄位的尺度(scale)是否相似,在餵資料進入模型訓練之前,決定是否需進行資料的正規化(Normalization)或標準化(Standardization)。
print( 'train' ) display( df_train.describe() ) print( 'test' ) display( df_test.describe() )
資料分析(Data Analysis)
在大致瞭解資料的基本態樣後,我們便可開始對資料做一些關聯性分析。由於是對整體資料進行分析,因此我們先使用 append( ) 函數將訓練集與測試集合併,方便後續一併修補或調整資料。
# 合併train及test的資料 df_data = df_train.append( df_test ) df_data
生還者的比率(Survival Ratio)
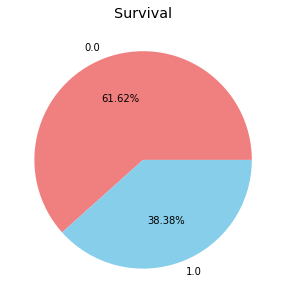
首先,我們分析生還者與罹難者的比例是否有明顯極大的落差,比如生還者的比例僅有 1%,若資料有極大的落差時,表示存在『數據不平衡』(Imbalanced Data)的問題,則後續需用特別的方法對資料進行抽樣。利用 value_counts( ) 函數,我們可以計算欄位中各相異類別的數量,船難中的生還者約佔全體乘客的 38.38%、罹難者約佔 61.62%。
Survived_Counts = df_data['Survived'].value_counts().reset_index() Survived_Counts.columns = ['Survived','Counts'] Survived_Counts
plt.figure( figsize=(10,5) ) df_data['Survived'].value_counts().plot( kind='pie', colors=['lightcoral','skyblue'], autopct='%1.2f%%' ) plt.title( 'Survival' ) # 圖標題 plt.ylabel( '' ) plt.show()
相關係數(Correlation)
利用 corr( ) 函數,計算特徵欄位彼此間的相關係數,可作為後續決定篩選哪些特徵欄位,來餵入模型進行訓練。觀察 Survived 欄位與其他特徵欄位的相關係數,發覺彼此間並無明顯的線性關係。
# Survied 與其他欄位間的相關係數
Corr_Matrix = df_train.corr() # 計算相關係數
Corr = Corr_Matrix.loc['Survived',:].sort_values()[:-1]
Corr = pd.DataFrame({ 'Survived':Corr })
Corr生存率(Survival Rate)
接下來,我們分別觀察性別(Sex)、票務艙(Pclass)、登船港口(Embarked)、兄弟姊妹配偶人數(SibSp)、父母子女人數(Parch)與生存率的關係。
# Sex性別、Pclass票務艙、Embarked登船港口、SibSp兄弟姊妹配偶人數、Parch父母子女人數
selected_cols = ['Sex','Pclass','Embarked','SibSp','Parch']
plt.figure( figsize=(10,len(selected_cols)*5) )
gs = gridspec.GridSpec(len(selected_cols),1)
for i, col in enumerate( df_data[selected_cols] ) :
ax = plt.subplot( gs[i] )
sns.countplot( df_data[col], hue=df_data.Survived, palette=['lightcoral','skyblue'] )
ax.set_yticklabels([])
ax.set_ylabel( 'Counts' )
ax.legend( loc=1 ) # upper right:1 ; upper left:2
for p in ax.patches:
ax.annotate( '{:,}'.format(p.get_height()), (p.get_x(), p.get_height()+1.5) )
plt.show()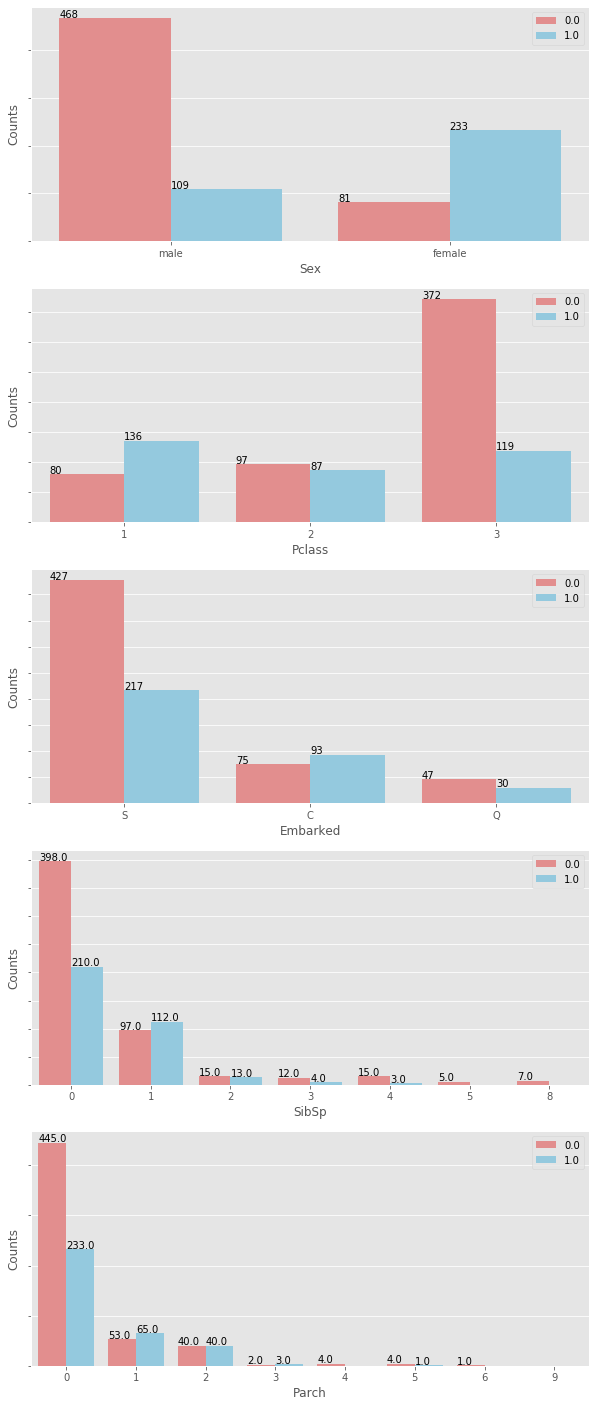
for col in selected_cols: l = ['Survived'] l.append(col) Survival_Rate = df_data[l].groupby(by=col).mean().round(4).reset_index() Survival_Rate.columns = [col,'Survival Rate(%)'] Survival_Rate['Survival Rate(%)'] = Survival_Rate['Survival Rate(%)'].map( lambda x:x*100 ) display( Survival_Rate )
透過上列的長條圖(Bar Plot)與統計表,我們可得到下列的觀察:
女性的生存率明顯高於男性;
票務艙(
Pclass )的生存率大小: Pclass 1 > Pclass 2 > Pclasss 3;登船港口(
Embarked )的生存率以 C 最高;當船上的兄弟姐妹配偶人數(
SibSp )有 1 人同行時,則生存率較高;當船上的父母子女人數(
Parch )為 1~3 人時,有較高的生存率。
由於 SibSp 與 Parch 欄位所記錄的人數皆屬於家庭成員,所以我們將兩者相加創造新的特徵欄位稱家庭人數(Family_Size),並觀察 Family_Size 與生存率的關係,發現當家庭人數為4時的生存率(約 72.4%)明顯高於其他人數。
# 創造新的特徵變數:家庭人數(Family_Size) df_data['Family_Size'] = df_data['SibSp'] + df_data['Parch'] + 1 Survival_Rate = df_data[['Family_Size','Survived']].groupby(by=['Family_Size']).agg(np.mean)*100 Survival_Rate.columns = ['Survival Rate(%)'] Survival_Rate.reset_index()
透過上列 Family_Size 欄位與生存率的關係,我們將 Family_Size 的生存率做級別的區分(3 表示生存率最高、1 為最低)。
df_data[ 'Family_Class' ] = np.nan df_data.loc[ df_data.Family_Size==0, 'Family_Class' ] = 2 df_data.loc[ (df_data.Family_Size>=1) & (df_data.Family_Size<=3), 'Family_Class' ] = 3 df_data.loc[ (df_data.Family_Size>=4) & (df_data.Family_Size<=6), 'Family_Class' ] = 2 df_data.loc[ (df_data.Family_Size>=7), 'Family_Class' ] = 1
另外,就整體而言,女性乘客的生存率(74%)明顯高於男性(19%),此時我們想更深入探討,在不同票務艙(Pclass)中的男性及女性,生存率是否也有明顯的差別?我們發現在 Pclass 1 與 Pclass 2 中,男女的生存率差異性更是明顯!!其中,在 Pclass 1 中的女性乘客生存率更是高達約 97%。
# Sex & Pclass Survival_Rate = df_data[['Sex','Pclass','Survived']].groupby(by=['Sex','Pclass']).agg(np.mean)*100 Survival_Rate.columns = ['Survival Rate(%)'] Survival_Rate.reset_index()
相似的手法,我們依據在不同艙等中的男女性生存率,給予不同的生存率級別(3最高、1最小):
df_data[ 'Sex_Pclass' ] = np.nan df_data.loc[ (df_data.Sex=='female') & (df_data.Pclass==1), 'Sex_Pclass' ] = 2 df_data.loc[ (df_data.Sex=='female') & (df_data.Pclass==2), 'Sex_Pclass' ] = 3 df_data.loc[ (df_data.Sex=='female') & (df_data.Pclass==3), 'Sex_Pclass' ] = 3 df_data.loc[ (df_data.Sex=='male') & (df_data.Pclass==1), 'Sex_Pclass' ] = 1 df_data.loc[ (df_data.Sex=='male') & (df_data.Pclass==2), 'Sex_Pclass' ] = 1 df_data.loc[ (df_data.Sex=='male') & (df_data.Pclass==3), 'Sex_Pclass' ] = 2
特徵工程(Feature Engineering)
在分析觀察完資料後,我們接著將處理一些無法直接餵入模型的特徵欄位,例如: Name 欄位為字串、Cabin 欄位中存有大量的缺漏值等。
(1) 字串欄位處理
Name (姓名)
首先,我們可先觀察 Name 欄位,發現可以擷取出稱謂(Title)的資訊,來幫助提升模型預測的準確度。一般在處理字串資料時,常用的函數有 split( )、repalce( ) 等來分割或取代字串中的文字,再比較程式語法化的方法可參考正規表示法(Regular Expression),這裏我們分別練習兩種方法:split( ) 與正規表示法,來擷取出 Name 欄位中的稱謂,產生的結果將僅有一個不同,其他皆完全相同:
# Method 1: split()
df_data['Title'] = df_data.Name.str.split(', ', expand=True)[1]
df_data['Title'] = df_data.Title.str.split('.', expand=True)[0]
df_data['Title'].unique()# Method 2: 正規表示法(Regular Expression) import re regex = re.compile( ' ([A-Za-z]+)\.' ) df_data['Title'] = df_data.Name.map( lambda x:regex.search(x)[0] ) # Dropping the first and the last words df_data['Title'] = df_data.Title.map( lambda x:x[1:][:-1] ) df_data['Title'].unique()
將同樣性別或關係的稱謂合併,避免產生某些稱謂僅有少數乘客,例如:Rev(Reverend)為牧師的尊稱、Countess為伯爵夫人等,影響模型的預測準確度。這裏我們將利用 replace( ) 函數,將上述擷取出的稱謂總歸為五類:Mr、Mrs、Miss、Master、Rare。
df_data['Title'] = df_data.Title.replace( ['Don','Rev','Dr','Major','Lady','Sir','Col','Capt','Countess','Jonkheer','Dona'], 'Rare' ) df_data['Title'] = df_data.Title.replace( ['Ms','Mlle'], 'Miss' ) df_data['Title'] = df_data.Title.replace( 'Mme', 'Mrs' ) df_data['Title'].unique()
# 刪除原始資料中的 Name 欄位 df_data.drop( 'Name', axis=1, inplace=True )
船票號碼(Ticket)
另外,我們合理假設 Ticket 中,前面英文字母的部份代表房間位於相同的區域中,我們再次利用 split( ) 及 repalce( ) 函數,來擷取 Ticket 字串中前面英文字母的部份文字訊息,作為乘客艙房的位置分區。
df_data['Ticket_info'] = df_data.Ticket.apply( lambda x:x.replace('.','').replace('/','').strip().split(' ')[0] if not x.isdigit() else 'X')
df_data['Ticket_info'].unique()# 刪除原始資料中的 Ticket 欄位 df_data.drop( 'Ticket', axis=1, inplace=True )
(2) 填補缺漏值(Missing Values)
針對存有缺漏值的欄位:Embarked、Fare、Cabin 及 Age 進行補值。一般而言,我們常選擇用平均值(Mean)、中位數(Median)或眾數(Mode)等補值,且利用 fillna( ) 函數來執行填補的動作,另外,較為進階的做法是透過機器學習模型進行補值,如:線性迴歸模型(Linear Regression)、決策樹(Decision Tree Regressor)等。
在補缺漏值前,我們再次查看整體資料的缺漏值分佈情況:
Missing_Counts( df_data.drop('Survived', axis=1) )票價(Fare) : 填補整體票價的中位數
df_data['Fare'].fillna( df_data.Fare.median(), inplace=True )
登船港口(Embarked) : 填補次數最多的港口 'S'
# 計算 Embarked 欄位中每個相異值的次數 display( df_data['Embarked'].value_counts() ) # 填補 Embarked 欄位的缺漏值 df_data['Embarked'].fillna( 'S', inplace=True )
年齡(Age) :
因為 Age 欄位的缺漏值佔比約有 20% ,不像前面 Fare 及 Embarked 欄位中僅有少數不到 1% 的缺漏值,因此我們所填補缺漏的值可能會影響預測的結果。此時,我們先藉由 Age 搭配 Sex 或 Pclass 欄位,觀察缺漏值分布的情況,檢視缺漏值是否集中發生在某類特別的乘客當中?
# 新增標註 Age 欄位是否為缺漏值的欄位(有缺漏標為0) df_data['isAge'] = df_data['Age'].isnull().map( lambda x:0 if x==True else 1 )
# 分別觀察 Age 與 Sex、Pclass 的缺漏值分布狀況 display( pd.crosstab( df_data.isAge, df_data.Sex, margins=True ) ) display( pd.crosstab( df_data.isAge, df_data.Pclass, margins=True ) )
fig, axs = plt.subplots(1,2,figsize=(14,5))
#plt.suptitle('Age')
plt.subplot(1,2,1)
sns.countplot( df_data.Sex, hue=df_data.isAge, palette=['lightcoral','skyblue'] )
plt.ylabel( 'Counts' )
plt.subplot(1,2,2)
sns.countplot( df_data.Pclass, hue=df_data.isAge, palette=['lightcoral','skyblue'] )
plt.ylabel( '' )
plt.show()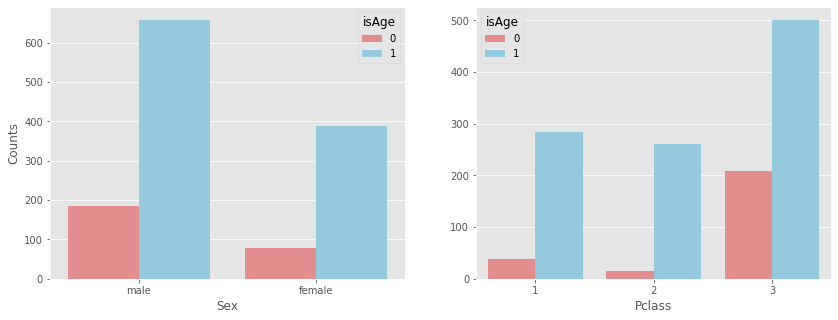
經觀察上表及圖後可知,Age 欄位的缺漏值明顯分佈在 Pclass 3 中,約佔 29.34%(=208/709),進一步觀察在 Pclass 1 及 Pclass 2 的乘客中,Age 欄位對於存活率是否有明顯的影響?
index_S = (df_data.isAge==1)&(df_data.Pclass!=3)&(df_data.Survived==1) index_D = (df_data.isAge==1)&(df_data.Pclass!=3)&(df_data.Survived==0) plt.figure( figsize=(14,5) ) sns.distplot( df_data.loc[index_S,'Age'], bins=20, color='blue', label='Survived' ) sns.distplot( df_data.loc[index_D,'Age'], bins=20, color='red', label='Dead' ) plt.title( 'Pclass = 1 or 2' ) plt.legend( ) plt.show( )
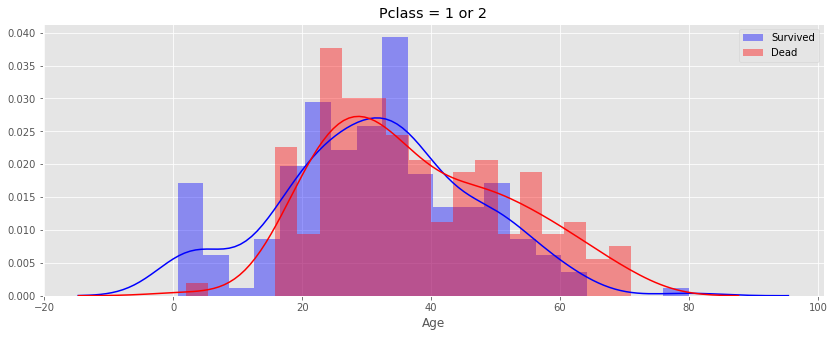
從上圖可觀察到,在 Pclass 1 及 Pclass 2 的乘客中,年齡約小於 17 歲的乘客中有明顯較高的生存率,若年齡超過 17 歲則生存率並無明顯的差別,所以我們可大膽假設 Age 欄位與生存率具有關聯性,另外,因為年齡與稱謂(Title)也有相當程度的關聯,因此,我們將先計算每個稱謂的年齡平均值,再用此平均值來填補每個 Title 中所對應 Age 欄位的缺漏值。
# 計算每個 Title 的年齡平均值及中位數 Age_Mean = df_data[['Title','Age']].groupby( by=['Title'] ).mean() Age_Median = df_data[['Title','Age']].groupby( by=['Title'] ).median() Age_Mean.columns = ['Age Mean'] Age_Median.columns = ['Age Median'] Age_Mean.reset_index( inplace=True ) Age_Median.reset_index( inplace=True ) display( Age_Median ) display( Age_Mean )
# 利用每個 Title 的年齡平均數,填補每個 Title 所對應 Age 的缺漏值 df_data.loc[(df_data.Age.isnull())&(df_data.Title=='Master'),'Age'] = Age_Mean.loc[Age_Mean.Title=='Master','Age Mean'][0] df_data.loc[(df_data.Age.isnull())&(df_data.Title=='Miss'),'Age'] = Age_Mean.loc[Age_Mean.Title=='Miss','Age Mean'][1] df_data.loc[(df_data.Age.isnull())&(df_data.Title=='Mr'),'Age'] = Age_Mean.loc[Age_Mean.Title=='Mr','Age Mean'][2] df_data.loc[(df_data.Age.isnull())&(df_data.Title=='Mrs'),'Age'] = Age_Mean.loc[Age_Mean.Title=='Mrs','Age Mean'][3] df_data.loc[(df_data.Age.isnull())&(df_data.Title=='Rare'),'Age'] = Age_Mean.loc[Age_Mean.Title=='Rare','Age Mean'][4] # 刪除 isAge 欄位 df_data.drop( 'isAge', axis=1, inplace=True )
填滿 Age 欄位的缺漏值後,我們將年齡特徵再區分成未滿17歲及17歲以上,未滿17歲的乘客標為1,17歲以上的乘客標為0。
# 乘客年齡是否未滿17歲(是:1;否:0) df_data[ 'is_Age_17' ] = (df_data.Age<17)*1 df_data
船艙號碼(Cabin) :
因爲整體 Cabin 欄位約有 77% 的缺漏值,我們在觀察 Cabin 欄位中的資料類別後,僅取出頭一個英文字母作為分類的標籤,其他缺漏的欄位以 NoCabin 表示。
# 觀察 Cabin 中的種類 df_data['Cabin'].unique()
# 取出 Cabin 中的第一個字母,如果為缺漏值,則以 NoCabin 表示 df_data['Cabin'] = df_data['Cabin'].apply( lambda x:str(x)[0] if not pd.isnull(x) else 'NoCabin' ) df_data['Cabin'].unique()
最後,在完成上述缺漏值的填補後,我們再次檢查是否還有缺漏值尚未填補到。
Missing_Counts( df_data.drop('Survived', axis=1) )(3) 離群值(Outlier)
因為離群值會明顯影響非樹狀模型的預測結果,例如:線性迴歸(Linear Regression)模型,因此,針對連續型的數值欄位,我們還需再檢視其資料的分布情況,透過觀察直方圖(Histogram)或盒鬚圖(Box Plot),可用來判斷欄位是否有離群值。
Reference : Understanding Boxplots
乘客票價(Fare) :
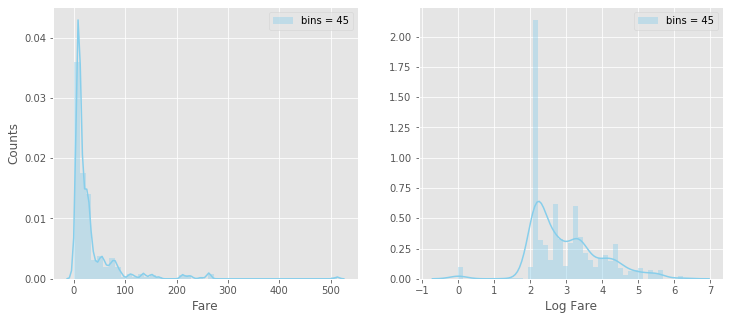
首先,我們先觀察 Fare 欄位的直方圖(Histogram)及盒鬚圖(Box Plot)資料分布狀況:
# 對 Fare 欄位取對數 df_data['LogFare'] = np.log1p( df_data.Fare ) # 直方圖(Histogram) fig, axs = plt.subplots( 1,2,figsize=(12,5) ) plt.subplot( 1,2,1 ) sns.distplot( df_data.Fare, kde=True, bins=45, color='skyblue', label='bins = 45' ) plt.xlabel( 'Fare' ) plt.ylabel( 'Counts' ) plt.legend( ) plt.subplot( 1,2,2 ) sns.distplot( df_data.LogFare, kde=True, bins=45, color='skyblue', label='bins = 45' ) plt.xlabel( 'Log Fare' ) plt.ylabel( '' ) plt.legend( ) plt.show()
# 盒鬚圖(Box Plot) fig, axs = plt.subplots( 1,2,figsize=(12,5) ) plt.subplot( 1,2,1 ) sns.boxplot( df_data.Fare, orient='h', color='skyblue' ) plt.xlabel( 'Fare' ) plt.subplot( 1,2,2 ) sns.boxplot( df_data.LogFare, orient='h', color='skyblue' ) plt.xlabel( 'Log Fare' ) plt.show()
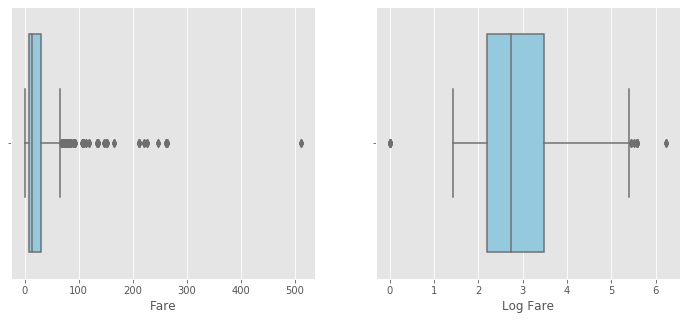
從上面直方圖及盒鬚圖可知,初步判斷 Fare 欄位可能存有離群值( i.e., 大於 Q3+1.5
# 計算 Fare 欄位各個百分位數(Percentile)
P_all = [ np.percentile( df_data.Fare, q=i ) for i in np.arange(0,101) ]
Pth_Percentile = pd.DataFrame( { 'Q':list(range(101)), 'Value':P_all } )
# The first、second and third quartile(i,e., the 25th、50th and 75th Percentile)
Q1 = Pth_Percentile.iloc[ 25, 1 ]
Q2 = Pth_Percentile.iloc[ 50, 1 ]
Q3 = Pth_Percentile.iloc[ 75, 1 ]
IQR = Q3 - Q1
print( f'Q1 = {Q1}' )
print( f'Q2 = {Q2} = Median' )
print( f'Q3 = {Q3}' )
print( f'Maximum = {df_data.Fare.max()}')
print( f'IQR = Q3 - Q1 = {IQR}' )
print( f'Q3 + 1.5IQR = {Q3+1.5*IQR}' )
# 依照四分位數,對 Fare 欄位進行分組
Fare_bin = [ 0, Q1, Q2, Q3, Q3+1.5*IQR, df_data.Fare.max() ]
df_data[ 'Fare_Group' ] = pd.cut( df_data.Fare.values, Fare_bin )
# 計算每個分組中的資料筆數
Group_Counts = df_data[ 'Fare_Group' ].value_counts().reset_index()
Group_Counts.columns = [ 'Fare_Group', 'Counts' ]
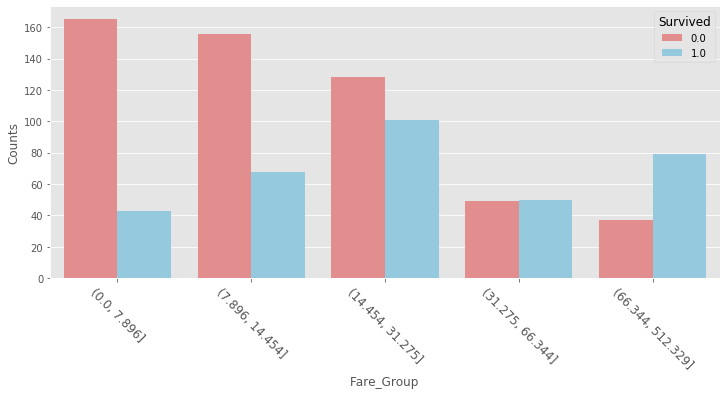
Group_Counts.sort_values( by='Fare_Group' )再次藉由長條圖及盒鬚圖,觀察不同的票價組別,彼此間生存率的差異性。
plt.subplots( figsize=(12,5) ) sns.countplot( df_data.Fare_Group, hue=df_data.Survived, palette=['lightcoral','skyblue'] ) plt.ylabel( 'Counts' ) plt.xticks( rotation=-45, fontsize=12 ) plt.show()
plt.subplots( figsize=(15,12) ) sns.boxplot( x='LogFare', y='Fare_Group', data=df_data, hue='Survived', orient='h', color='skyblue' ) plt.yticks( rotation=-30, fontsize=15 ) plt.show()
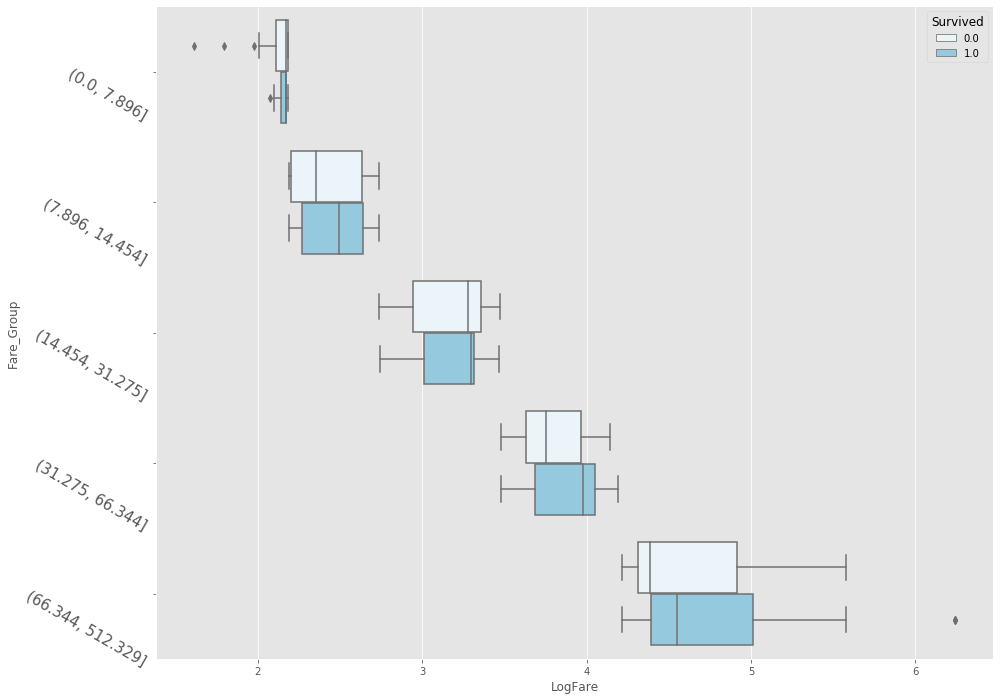
從上圖可明顯觀察出,票價組別越高生存率相對越大,且每一票價組別中,生還者的票價中位數皆高於罹難者的票價中位數;所以,我們可大膽推測 Fare 與生存率有相關性,Fare 越高生存機率越大,且對 Fare 欄位僅做對數轉換並不做離群值的處理。
# 刪除 Fare_Group 欄位 df_data.drop( ['Fare','Fare_Group'], axis=1, inplace=True )
(4) 獨熱編碼(OneHot Encoding)、標籤編碼(Label Encoding)
對於定性且無序的特徵欄位,例如:性別、顏色、國家別等,我們可利用 get_dummies( ) 函數執行獨熱編碼,將其轉換成定量資料,這裏我們對 Embarked 欄位做獨熱編碼;另外,因為女性的生存率明顯高於男性,故我們對 Sex 欄位做標籤編碼。
登船港口(Embarked) :
# OneHot Encoding OneHot_Embarked = pd.get_dummies( df_data.Embarked, prefix='Embarked' ) # 合併 Embarked 編碼後的欄位 df_data = pd.concat( [ df_data, OneHot_Embarked ], axis=1 ) df_data.drop( 'Embarked', axis=1, inplace=True )
性別(Sex) :
# Label Encoding
Sex_mapping = { 'male':0, 'female':1 }
df_data[ 'Sex' ] = df_data.Sex.map( Sex_mapping )訓練集(Train)與測試集(Test)
在完成前述的資料分析及特徵工程後,我們就快可以把資料餵入模型進行訓練了!在此之前的最後一個注意步驟,就是需確認每個欄位皆為數值型態,且將資料分割回訓練集(train)與測試集(test)。所以,此時我們先檢視特徵工程後的資料,觀察是否還有需要處理的欄位:
# 檢視特徵工程後的資料
print( f'Shape of data after feature engineering = {df_data.shape}' )
df_data.head()(1) 類別型態欄位轉為整數
檢視後發現,因為我們之前有處理過字串欄位,所以資料中還存有 4 欄類別型態的欄位:Cabin、Embarked、Title、Ticket_info,因此,我們也需要將它們轉換成數值型態欄位:
for col in ['Title','Ticket_info','Cabin']:
df_data[col] = df_data[col].astype('category').cat.codes
df_data.head()(2) 產生訓練集(Train)與測試集(Test)
最後,我們將整體資料分割回訓練集與測試集兩部份,訓練集用來餵入模型進行訓練,測試集則為模型最終要預測的結果,此外,在分割產出資料後,我們刪除與生存率無毫關聯性的欄位 PassengerId。
# 產生訓練集和測試集
Train = df_data[ pd.notnull(df_data.Survived) ]
Test = df_data[ pd.isnull(df_data.Survived) ]
# 訓練集刪除 PassengerId 欄位;
# 測試集刪除 PassengerId 與 Survived 欄位
Train.drop( ['PassengerId'], axis=1, inplace=True )
Test.drop( ['PassengerId','Survived'], axis=1, inplace=True )
# 將測試集中的標籤欄位 Survived 單獨拆出
Y_Train = Train.Survived
X_Train = Train.drop( ['Survived'], axis=1 )
print( f'Shape of X_Train = {X_Train.shape}' )
print( f'Shape of Y_Train = {Y_Train.shape}' )
print( f'Shape of Test = {Test.shape}' )特徵重要性(Feature Importance)
我們使用最基本的樹狀模型 - 決策樹(Decision Tree),來評估特徵欄位對於標籤欄位(Survived)的重要性,目的是幫助我們篩選較具關鍵性的特徵欄位,提升模型的預測能力。評估特徵重要性的方法並非僅侷限於決策樹,另外其他常見的手法有:相關係數(Correlation)、Lasso等。
# 建立決策樹模型
DTC = RandomForestClassifier( )
# 自變數、應變數進行擬合
DTC.fit( X_Train, Y_Train )
# 排序特徵重要性(由大到小)
col_names = X_Train.columns
importances = DTC.feature_importances_
Feature_Rank = pd.DataFrame( { 'Feature_Name':col_names, 'Importance':importances } )
Feature_Rank.sort_values( by='Importance', ascending=False, inplace=True )
Feature_Rank建立模型
在完成評估特徵重要性後,我們選擇使用隨機森林(Random Forest)來預測資料。由於在森林中每一棵樹的生成方法為拔靴法(Boostrap),表示每一棵樹並不會用到所有的訓練集資料來生成,而未使用的樣本稱為袋外樣本(Out of Bag Sample),其可用來評估預測的準確度,每一顆樹皆以這種方式生成,最後對所有樹的準確度取平均值,這便是隨機森林的特性。
Reference:RandomForestClassifier
# 隨機森林參數: # n_estimators: 樹的數量(default=10)。 # min_samples_leaf: 最終葉節點最少樣本數(default=1); # 當樣本不大時,可不設定使用預設,若樣本數量非常大時,則推薦增加此參數值。 # min_samples_split:節點再劃分時所需的最小樣本數(default=2); # 當樣本不大時,可不設定使用預設,若樣本數量非常大時,則推薦增加此參數值。 # oob_score: 是否採用袋外樣本(out-of-bag samples)來評估模型的準確度(default=False)。 RFC = RandomForestClassifier( n_estimators = 1000, min_samples_split = 20, min_samples_leaf = 1, oob_score = True, random_state = 1, n_jobs = -1 )
訓練模型
餵入訓練集資料(X_Train,Y_Train)訓練隨機森林(Random Forest)模型。一般而言,為了衡量模型的預測能力,在訓練模型之前,我們還會從訓練集中抽取出一小部份作為驗證集(Validation),用來評估模型的準確度,而剩下沒被抽取到的資料則用來訓練模型,另外,為避免只參考某一特定的抽樣驗證結果,導致模型產生偏差,我們會藉由交叉驗證(Cross Validation),來評估模型的準確度是否能達到我們要求的水準。
因為隨機森林可藉由前述所提的袋外樣本評估準確度,因此這裏我們便不需進行交叉驗證;然而,我們還想知道特徵欄位的多寡對於模型準確度的影響,所以,先把所有的欄位餵入模型進行訓練:
# 訓練模型
RFC.fit( X_Train, Y_Train )
print( 'oob_score = {:.6f}'.format(RFC.oob_score_) )將所有的特徵欄位餵入模型進行訓練,訓練完成的模型準確率約 83.3%;接下來,我們試著參考上述特徵重要性的結果,只選擇部份特徵欄位來訓練模型,觀察這樣的模型準確度是否能有所提升?
RFC_2 = RandomForestClassifier( n_estimators = 1000,
min_samples_split = 20,
min_samples_leaf = 1,
oob_score = True,
random_state = 1,
n_jobs = -1 )
# 篩選部份特徵欄位餵入模型進行訓練
SelectedFeatures = ['Age','Sex','LogFare','Title','Pclass','Sex_Pclass']
RFC_2.fit( X_Train[SelectedFeatures], Y_Train )
print( f'Selected Features :\n {SelectedFeatures}' )
print( 'oob_score = {:.6f}'.format(RFC_2.oob_score_) )經觀察,只篩選部份特徵欄位所訓練出的模型準確率約 84.4%,略高於所有特徵欄位所訓練出的模型,從這我們可得到一個寶貴的經驗,就是適當的挑選出關鍵性的特徵欄位進行訓練,對於模型的準確度將會有所提升。
測試集預測
最後,將我們訓練完成的模型用來預測測試集資料,且上傳預測結果至 Kaggle,終於大公告成了!!
# 預測測試集資料 Test_pred = RFC_2.predict( Test[SelectedFeatures] ) # 檢視預測罹難或生還的機率 #print( RFC_2.predict_proba(Test[SelectedFeatures]) ) # 提交檔案 submit['Survived'] = Test_pred.astype(int) submit.to_csv( 'Titanic_RandomForest.csv', index=False ) print( f'預測結果:' ) submit
總結
藉由 Kaggle 上鐵達尼號生存預測比賽,我們簡單地分享有關資料的分析及處理技巧,除希望文中的程式碼範本能幫助初心者們快速上手外,更希望能使讀者瞭解一個機器學習專案的基本構思及流程,通常一個機器學習專案,我們會耗費絕大部分的時間在資料分析與特徵工程上,模型的選用及調整參數是不太需要花時間的。因此,一個專案要能順利進行,除需具備熟練的程式語言外,該領域的專業知識及實務經驗,更是一大關鍵的因素。
最後,對於鐵達尼號生存預測比賽有興趣的初心者們,不妨再試著做更多不同的觀察及嘗試,相信你將會獲得多元的收穫與經驗!針對本文的內容,若讀者們有發現任何的錯誤或疑問,非常歡迎您來信給予建議及討論,讓我們一同來學習成長!
歡迎未來有興趣一起參與學習的朋友們,一起追蹤我們粉絲專頁、加入學習社團,並持續關注 AI . FREE Team 部落格,如有進一步問題或是交流需求,歡迎透過粉專 or email 聯絡我們喔!(AI.Free.Team@gmail.com)
相關資訊:
認識自由團隊:https://goo.gl/D2in5A
加入學習社群:https://goo.gl/k98CBy
企業合作專區:https://goo.gl/osGHhK
自由學習平台:https://goo.gl/ALVKKF
【AI.Free Team 介紹影片】
https://www.youtube.com/watch?v=nEOi9qk35KA
